Introduction of Recursion and Dynamic Programming:

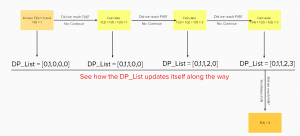
Recursion is the process in which a function calls itself until the base cases are reached. And during the process, complex situations will be traced recursively and become simpler and simpler. The whole structure of the process is tree-like. Recursion does not store any value until reaching the final stage(base case).

And Dynamic Programming is mainly an optimization compared to simple recursion. The main idea is to decompose the original question into repeatable patterns and then store the results as many sub-answers. Therefore, we do not have to re-compute the pre-step answers when needed later. In terms of big O, this optimization method generally reduces time complexities from exponential to polynomial.

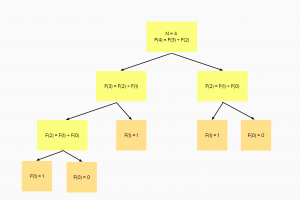
How to write a recursion/dynamic programming script?

Dynamic Programming and Recursion are very similar-

1. Both recursion and dynamic programming are starting with the base case where we initialize the start.
2. After we wrote the base case, we will try to find any patterns followed by the problem’s logic flow. Once we find it, we are basically done.
3. The main difference is that, for recursion, we do not store any intermediate values whereas dynamic programming does utilize that

Problem Statement:

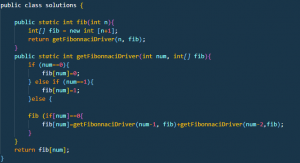
Example: Leetcode 509. Fibonacci Number

Problem Prompt-

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

F[0] = 0 as the first number

F[1] = 1 as our second number

And the number after that is easy to compute:

F[n] = F[n-1] + F[n-2]

Examples-

How could we find F[n] with a given n?

 Examples-

If this is the very first time heard something called Fibonacci Number, do not worry, here are some easy examples to understand the question:

Given n = 2, F[2] = F[1] + F[0] = 0 + 1 = 1

Given n = 3, F[3] = F[2] + F[1] = 1+ 2= 3

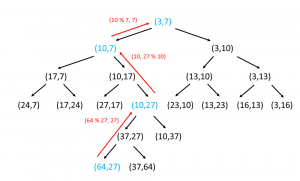
Fibonacci Tree with recursive Approach leads to O(2^n) time complexity, but this is too bad for larger problems this is okay for small problems.

To Optimize the time complexity of Fibonacci recursive problems we use memoization and dynamic programming.

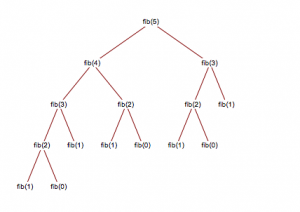
The Following Tree is having multiple same recursive calls so that’s why we optimize the following approach using memoization and dynamic programming where we need to remove the recursive calls and store them in an array.